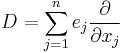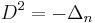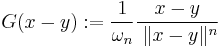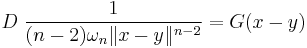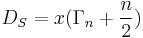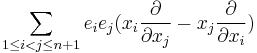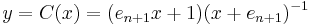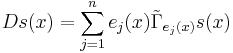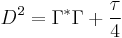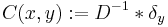Clifford analysis
Clifford analysis, using Clifford algebras named after William Kingdon Clifford, is the study of Dirac operators, and Dirac type operators in analysis and geometry, together with their applications. Examples of Dirac type operators include, but are not limited to, the Hodge-Dirac operator, 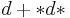 on a Riemannian manifold, the Dirac operator in euclidean space and its inverse on
on a Riemannian manifold, the Dirac operator in euclidean space and its inverse on 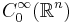 and their conformal equivalents on the sphere, the Laplacian in euclidean n-space and the Atiyah-Singer-Dirac operator on a spin manifold, Rarita-Schwinger/ Stein-Weiss type operators, conformal Laplacians, spinorial Laplacians and Dirac operators on Spinc manifolds, systems of Dirac operators, the Paneitz operator, Dirac operators on hyperbolic space, the hyperbolic Laplacian and Weinstein equations.
and their conformal equivalents on the sphere, the Laplacian in euclidean n-space and the Atiyah-Singer-Dirac operator on a spin manifold, Rarita-Schwinger/ Stein-Weiss type operators, conformal Laplacians, spinorial Laplacians and Dirac operators on Spinc manifolds, systems of Dirac operators, the Paneitz operator, Dirac operators on hyperbolic space, the hyperbolic Laplacian and Weinstein equations.
Contents |
Euclidean space
In Euclidean space the Dirac operator has the form
where e1...en is an orthonormal basis for Rn, and Rn is considered to be embedded in a complex Clifford algebra, Cℓn(C) so that ej2 = -1.
This gives
where Δn is the Laplacian in n-euclidean space.
The fundamental solution to the euclidean Dirac operator is
where ωn is the surface area of the unit sphere Sn-1.
Note that
where 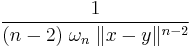 is the fundamental solution to Laplace's equation for n ≥ 3.
is the fundamental solution to Laplace's equation for n ≥ 3.
The most basic example of a Dirac operator is the Cauchy-Riemann operator 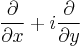 in the complex plane. Indeed many basic properties of one variable complex analysis follow through for many first order Dirac type operators. In euclidean space this includes a Cauchy Theorem, a Cauchy integral formula, Morera's Theorem, Taylor series, Laurent series and Liouville Theorem. In this case the Cauchy kernel is
in the complex plane. Indeed many basic properties of one variable complex analysis follow through for many first order Dirac type operators. In euclidean space this includes a Cauchy Theorem, a Cauchy integral formula, Morera's Theorem, Taylor series, Laurent series and Liouville Theorem. In this case the Cauchy kernel is 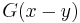 . The proof of the Cauchy integral formula is the same as in one complex variable and makes use of the fact that each non-zero vector
. The proof of the Cauchy integral formula is the same as in one complex variable and makes use of the fact that each non-zero vector  in euclidean space has a multiplicative inverse in the Clifford algebra, namely
in euclidean space has a multiplicative inverse in the Clifford algebra, namely 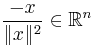 . Up to a sign this inverse is the Kelvin inverse of
. Up to a sign this inverse is the Kelvin inverse of  . Solutions to the euclidean Dirac equation
. Solutions to the euclidean Dirac equation 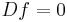 are called (left) monogenic functions. Monogenic functions are special cases of harmonic spinors on a spin manifold.
are called (left) monogenic functions. Monogenic functions are special cases of harmonic spinors on a spin manifold.
In 3 and 4 dimensions Clifford analysis is sometimes referred to as quaternionic analysis. When n=4 the Dirac operator is sometimes referred to as the Cauchy-Riemann-Fueter operator. Further some aspects of Clifford analysis are referred to as hypercomplex analysis.
Clifford analysis has analogues of Cauchy transforms, Bergman kernels, Szegő kernels, Plemelj operators, Hardy spaces, a Kerzman-Stein formula and a Π, or Beurling-Ahlfors, transform. These have all found applications in solving boundary value problems, including moving boundary value problems, singular integrals and classic harmonic analysis. In particular Clifford analysis has been used to solve, in certain Sobolev spaces, the full water wave problem in 3-D. This method works in all dimensions greater than 2.
Much of Clifford analysis works if we replace the complex Clifford algebra by a real Clifford algebra, 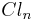 . This is not the case though when we need to deal with the interaction between the Dirac operator and the Fourier transform.
. This is not the case though when we need to deal with the interaction between the Dirac operator and the Fourier transform.
The Fourier Transform
When we consider upper half space 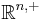 with boundary
with boundary 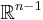 , the span of
, the span of 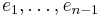 , under the Fourier transform the symbol of the Dirac operator
, under the Fourier transform the symbol of the Dirac operator 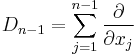 is
is 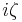 where
where  .
.
In this setting the Plemelj formulas are 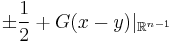 and the symbols for these operators are, up to a sign,
and the symbols for these operators are, up to a sign, 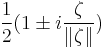 . These are projection operators, otherwise known as mutually annihilating idempotents, on the space of Cln(C) valued square integrable functions on Rn-1.
. These are projection operators, otherwise known as mutually annihilating idempotents, on the space of Cln(C) valued square integrable functions on Rn-1.
Note that 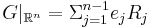 where
where 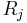 is the
is the  -th Riesz potential,
-th Riesz potential, 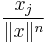 . As the symbol of
. As the symbol of 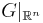 is
is 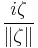 it is easily determined from the Clifford multiplication that
it is easily determined from the Clifford multiplication that 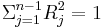 . So the convolution operator
. So the convolution operator 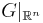 is a natural generalization to euclidean space of the Hilbert transform.
is a natural generalization to euclidean space of the Hilbert transform.
Suppose 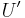 is a domain in
is a domain in 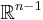 and
and 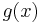 is a
is a 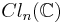 valued real analytic function. Then
valued real analytic function. Then  has a Cauchy-Kovalevskaia extension to the Dirac equation on some neighborhood of
has a Cauchy-Kovalevskaia extension to the Dirac equation on some neighborhood of 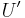 in
in 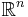 . The extension is explicitly given by
. The extension is explicitly given by 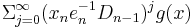 .
.
When this extension is applied to the variable  in
in 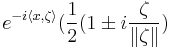 we get that
we get that 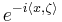 is the restriction to
is the restriction to 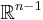 of
of 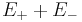 where
where 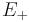 is a monogenic function in upper half space and
is a monogenic function in upper half space and 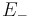 is a monogenic function in lower half space.
is a monogenic function in lower half space.
There is also a Paley-Weiner theorem in n-euclidean space arising in Clifford analysis.
Conformal Structure
Many Dirac type operators have a covariance under conformal change in metric. This is true for the Dirac operator in euclidean space, and the Dirac operator on the sphere under Moebius transformations. Consequently this holds true for Dirac operators on conformally flat manifolds and conformal manifolds which are simultaneously spin manifolds.
Cayley transform (stereographic projection)
The Cayley transform or stereographic projection from 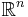 to the unit sphere
to the unit sphere 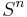 transforms the euclidean Dirac operator to a spherical Dirac operator
transforms the euclidean Dirac operator to a spherical Dirac operator 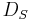 . Explicitly
. Explicitly
where 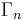 is the spherical Beltrami-Dirac operator
is the spherical Beltrami-Dirac operator
and 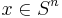 .
.
The Cayley transform over n-space is
where 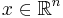 . Its inverse is
. Its inverse is
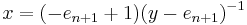 .
.
For a function  defined on a domain
defined on a domain  in n-euclidean space and a solution to the Dirac equation, then
in n-euclidean space and a solution to the Dirac equation, then 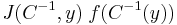 is annihilated by
is annihilated by 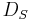 , on
, on 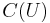 where
where 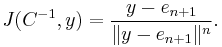
Further 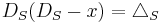 , the conformal Laplacian or Yamabe operator on
, the conformal Laplacian or Yamabe operator on 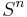 . Explicitly
. Explicitly 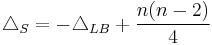 where
where 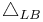 is the Laplace-Beltrami operator on
is the Laplace-Beltrami operator on 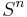 . The operator
. The operator 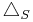 is, via the Cayley transform, conformally equivalent to the euclidean Laplacian. Also
is, via the Cayley transform, conformally equivalent to the euclidean Laplacian. Also 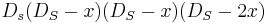 is the Paneitz operator,
is the Paneitz operator, 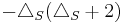 , on the n-sphere. Via the Cayley transform this operator is conformally equivalent to the bi-Laplacian,
, on the n-sphere. Via the Cayley transform this operator is conformally equivalent to the bi-Laplacian, 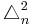 . These are all examples of operators of Dirac type.
. These are all examples of operators of Dirac type.
Moebius transform
A Moebius transform over n-euclidean space can be expressed as 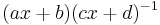 where
where  ,
,  ,
,  and
and  ∈ Cln and satisfy certain constraints. The associated 2 × 2 matrix is called an Ahlfors-Vahlen matrix. If
∈ Cln and satisfy certain constraints. The associated 2 × 2 matrix is called an Ahlfors-Vahlen matrix. If 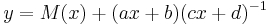 and
and 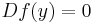 then
then 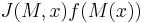 is a solution to the Dirac equation where
is a solution to the Dirac equation where 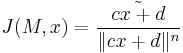 and
and 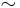 is a basic antiautomorphism acting on the Clifford algebra. The operators
is a basic antiautomorphism acting on the Clifford algebra. The operators 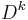 , or Δnk/2 when
, or Δnk/2 when  is even, exhibit similar covariances under Moebius transform including the Cayley transform.
is even, exhibit similar covariances under Moebius transform including the Cayley transform.
When 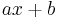 and
and 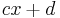 are non-zero they are both members of the Clifford group.
are non-zero they are both members of the Clifford group.
As 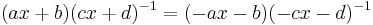 then we have a choice in sign in defining
then we have a choice in sign in defining 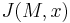 . This means that for a conformally flat manifold
. This means that for a conformally flat manifold  we need a spin structure on
we need a spin structure on  in order to define a spinor bundle on whose sections we can allow a Dirac operator to act. Explicit simple examples include the n-cylinder, the Hopf manifold obtained from n-euclidean space minus the origin, and generalizations of k-handled toruses obtained from upper half space by factoring it out by actions of generalized modular groups acting on upper half space totally discontinuosly. A Dirac operator can be introduced in these contexts. These Dirac operators are special examples of Atiyah-Singer-Dirac operators.
in order to define a spinor bundle on whose sections we can allow a Dirac operator to act. Explicit simple examples include the n-cylinder, the Hopf manifold obtained from n-euclidean space minus the origin, and generalizations of k-handled toruses obtained from upper half space by factoring it out by actions of generalized modular groups acting on upper half space totally discontinuosly. A Dirac operator can be introduced in these contexts. These Dirac operators are special examples of Atiyah-Singer-Dirac operators.
The Atiyah-Singer-Dirac Operator
Given a spin manifold,  , with a spinor bundle
, with a spinor bundle  then given a smooth section
then given a smooth section 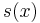 in
in  then in terms of a local orthonormal basis e1(x)... en(x) of the tangent bundle of
then in terms of a local orthonormal basis e1(x)... en(x) of the tangent bundle of  the Atiyah-Singer-Dirac operator acting on
the Atiyah-Singer-Dirac operator acting on  is defined to be
is defined to be
where 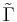 is the lifting to
is the lifting to  of the Levi-Civita connection on
of the Levi-Civita connection on  . When
. When  is n-euclidean space we return to the euclidean Dirac operator.
is n-euclidean space we return to the euclidean Dirac operator.
From an Atiyah-Singer-Dirac operator  we have the Lichnerowicz formula
we have the Lichnerowicz formula
where  is the scalar curvature on the manifold, and
is the scalar curvature on the manifold, and 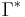 is the adjoint of
is the adjoint of  . The operator
. The operator 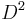 is known as the spinorial Laplacian.
is known as the spinorial Laplacian.
If  is compact and
is compact and 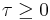 and
and 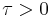 somewhere then there are no non-trivial harmonic spinors on the manifold. This is Lichnerowicz' Theorem. It is readily seen that that Lichnerowicz' Theorem is a generalization of Liouville's Theorem from one variable complex analysis. This allows us to note that over the space of smooth spinor sections the operator
somewhere then there are no non-trivial harmonic spinors on the manifold. This is Lichnerowicz' Theorem. It is readily seen that that Lichnerowicz' Theorem is a generalization of Liouville's Theorem from one variable complex analysis. This allows us to note that over the space of smooth spinor sections the operator  is invertible for such a manifold.
is invertible for such a manifold.
In the cases where the Atiyah-Singer-Dirac operator is invertible on the space of smooth spinor sections with compact support one may introduce
where 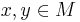 with
with 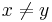 and
and 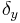 is the Dirac delta function evaluated at
is the Dirac delta function evaluated at  . This gives rise to a Cauchy kernel, which is the fundamental solution to this Dirac operator. From this one may obtain a Cauchy integral formula for harmonic spinors. With this kernel much of what is described in the first section of this entry carries through for invertible Atiyah-Singer-Dirac operators.
. This gives rise to a Cauchy kernel, which is the fundamental solution to this Dirac operator. From this one may obtain a Cauchy integral formula for harmonic spinors. With this kernel much of what is described in the first section of this entry carries through for invertible Atiyah-Singer-Dirac operators.
Using Stokes' theorem, or otherwise, one can further determine that under a conformal change of metric the Dirac operators associated to each metric are proportional to each other, and consequently so are their inverses, if they exist.
All of this provides potential links to Atiyah-Singer index theory and other aspects of geometric analysis involving Dirac type operators.
Hyperbolic Dirac Type Operators
In Clifford analysis one also considers differential operators on upper half space, the disc, or hyperbola with respect to the hyperbolic, or Poincaré metric.
For upper half space one splits the Clifford algebra, 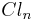 into
into 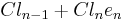 . So for
. So for 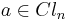 one may express
one may express  as
as 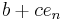 with
with  ,
, 
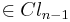 . One then has projection operators
. One then has projection operators  and
and  defined as follows
defined as follows 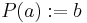 and
and 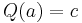 . The Hodge-Dirac operator acting on a function
. The Hodge-Dirac operator acting on a function  with respect to the hyperbolic metric in upper half space is now defined to be
with respect to the hyperbolic metric in upper half space is now defined to be
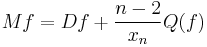 .
.
In this case
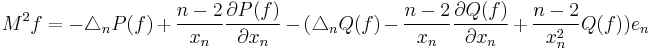 .
.
The operator 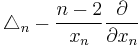 is the Laplacian with respect to the Poincaré metric while the other operator is an example of a Weinstein operator.
is the Laplacian with respect to the Poincaré metric while the other operator is an example of a Weinstein operator.
The hyperbolic Laplacian is invariant under actions of the conformal group, while the hyperbolic Dirac operator is covariant under such actions.
Rarita-Schwinger/ Stein-Weiss Operators
Rarita-Schwinger operators, also known as Stein-Weiss operators, arise in representation theory for the Spin and Pin groups. The operator 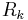 is a conformally covariant first order differential operator. Here
is a conformally covariant first order differential operator. Here 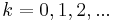 . When
. When 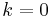 then the Rarita-Schwinger operator is just the Dirac operator. In representation theory for the orthogonal group,
then the Rarita-Schwinger operator is just the Dirac operator. In representation theory for the orthogonal group, 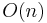 it is common to consider functions taking values in spaces of homogeneous harmonic polynomials. When one refines this representation theory to the double covering
it is common to consider functions taking values in spaces of homogeneous harmonic polynomials. When one refines this representation theory to the double covering 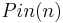 of
of 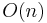 one replaces spaces of homogeneous harmonic polynomials by spaces of k homogeneous polynomial solutions to the Dirac equation, otherwise known as
one replaces spaces of homogeneous harmonic polynomials by spaces of k homogeneous polynomial solutions to the Dirac equation, otherwise known as  monogenic polynomials. One considers a function
monogenic polynomials. One considers a function 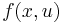 where
where 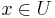 a domain in
a domain in 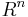 and
and  varies over
varies over 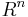 . Further
. Further 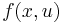 is a k-monogenic polynomial in
is a k-monogenic polynomial in  . Now apply the Dirac operator
. Now apply the Dirac operator 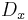 in
in  to
to 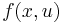 . Now as the Clifford algebra is not commutative
. Now as the Clifford algebra is not commutative 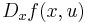 then this function is no longer
then this function is no longer  monogenic but is a homogeneous harmonic polynomial in
monogenic but is a homogeneous harmonic polynomial in  . Now for each harmonic polynomial
. Now for each harmonic polynomial 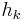 homogeneous of degree
homogeneous of degree  there is an Almansi-Fischer decomposition
there is an Almansi-Fischer decomposition 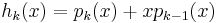 where
where 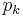 and
and 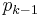 are respectively
are respectively  and
and 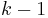 monogenic polynomials. Let
monogenic polynomials. Let  be the projection of
be the projection of 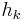 to
to 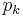 then the Rarita Schwinger operator is defined to be
then the Rarita Schwinger operator is defined to be 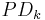 , and it is denoted by
, and it is denoted by 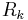 . Using Euler's Lemma one may determine that
. Using Euler's Lemma one may determine that 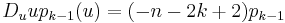 . So
. So 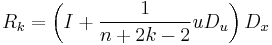 .
.
See also
- Clifford algebra
- Complex spin structure
- Conformal manifold
- Conformally flat manifold
- Dirac operator
- Poincaré metric
- Spin structure
- Spinor bundle
References
- Ahlfors, L. (1981), Moebius Transformations in Several Dimensions, University of Minnesota: Ordway Lecture Notes.
- Ahlfors, L. (1986), "Mobius transformations in Rn expressed through 2 × 2 matrices of Clifford numbers", Complex Variables 5: 215–224.
- Brackx, F.; Delanghe, R.; Sommen, F. (1982), Clifford Analysis, London: Pitman Research Notes in Mathematics, Longman, ISBN 0273085352.
- Bures, J.; Sommen, F.; Soucek, V.; VanLancker, P. (2001), "Rarita-Schwinger type operators in Clifford analysis", Journal of Functional Analysis 185 (2): 425–455, doi:10.1006/jfan.2001.3781.
- Colombo, F.; Sabadini, I.; Sommen, F.; Struppa, D. (2004), Analysis of Dirac Systems and Computational Algebra, Basel: Progress in Mathematical Physics, Birkhauser Verlag, ISBN 0-8176-4255-2.
- Eastwood, M.; Ryan, J. (2007), "Aspects of Dirac operators in analysis", Milan Journal of Mathematics 75 (1): 91–116, doi:10.1007/s00032-007-0077-5.
- Jefferies, B. (2004), Spectral Properties of Noncommuting Operators, Heidelberg: Lecture Notes in Mathematics, no 1843, Springer Verlag, ISBN 3-540-21923-4.
- Krausshar, R. S. (2004), Generalized Analytic Automorphic Forms in Hypercomplex Space, Basel: Frontiers in Mathematics, Birkhauser Verlag, ISBN 3-7643-7059-9.
- Lawson, H. B.; Michelsohn, M.-L. (1989), Spin Geometry, Princeton Mathematical Series, No 38, Princeton University Press, ISBN 0-691-08542-0.
- McIntosh, A. (1996), "Clifford algebras, Fourier theory, singular integrals, and harmonic functions on Lipschitz domains", in Ryan, J., Clifford Algebras in Analysis and Related Topics, Boca Raton: Studies in Advanced Mathematics, CRC Press, pp. 33–87, ISBN 0-8493-8481-8.
- Mitrea, M. (1994), Singular Integrals, Hardy Spaces and Clifford Wavelets, Heidelberg: Lecture Notes in Mathematics, No 1575, Springer Verlag, ISBN 0387578846.
- Roe, J. (1998), Elliptic Operators, Topology and Asymptotic Methods, 2nd Edition, Harlow: Pitman Research Notes in Mathematics, No 395, Longman, ISBN 0-582-32502-1.
- Ryan, J. (1996), Clifford Algebras in Analysis and Related Topics, Boca Raton: Studies in Advanced Mathematics, CRC Press, ISBN 0-8493-8481-8.
- Stein, E.; Weiss, G. (1968), "Generalizations of the Cauchy Riemann equations and representations of the rotation group", American Journal of Mathematics (The Johns Hopkins University Press) 90 (1): 163–196, doi:10.2307/2373431, JSTOR 2373431.
- Sudbery, A. (1979), "Quaternionic analysis", Mathematical Proceedings of the Cambridge Philosophical Society 85 (02): 199–225, Bibcode 1979MPCPS..85..199S, doi:10.1017/S0305004100055638.
- Tao, T. (1996), "Convolution operators on Lipschitz graphs with harmonic kernels", Advances in Applied Clifford Algebras 6: 207–218.
- Wu, S. (1999), "Well-posedness in Sobolev spaces of the full water wave problem in 3-D", Journal of the American Mathematical Society 12 (02): 445–495, doi:10.1090/S0894-0347-99-00290-8.